
Una feroce polemica tra fisici sull’idea di Hawking secondo la quale l’universo non ha avuto inizio. Una recente sfida alla più grande idea di Stephen Hawking – in base alla quale l’universo potrebbe provenire dal nulla – ha visto fisici e cosmologi prendere posizione su due fronti contrapposti
Nel 1981, molti dei più importanti cosmologi del mondo si riunirono presso la Pontificia Accademia delle Scienze, una testimonianza della vicinanza tra scienza e teologia, situati in un’elegante villa nei giardini del Vaticano. Stephen Hawking scelse quella sede per presentare ciò che in seguito avrebbe considerato come la sua idea più importante: una proposta su come l’universo potesse essere sorto dal nulla.
Prima delle parole di Hawking, la più accreditata delle risposte alla domanda sull’origine dell’universo, la teoria del Big Bang (all’epoca chiamata teoria dell’atomo primigenio), era stata presentata 50 anni prima dal fisico belga e sacerdote cattolico Georges Lemaître, che in seguito fu presidente dell’Accademia delle scienze vaticana – riavvolge l’espansione dell’universo in un punto di energia caldo e denso.
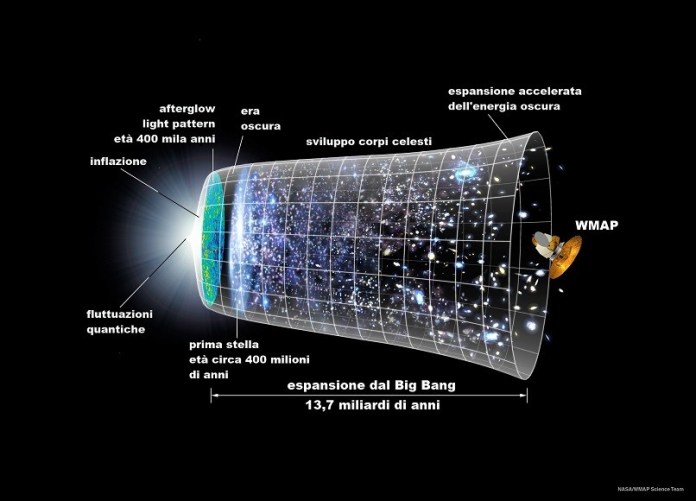
Ma da dove veniva l’energia iniziale?
La teoria del Big Bang ha avuto altri problemi. I fisici hanno capito che un fascio di energia in espansione si sarebbe trasformato in un disordine confuso piuttosto che nell’enorme cosmo liscio che gli astronomi moderni osservano. Nel 1980, l’anno prima del discorso di Hawking, il cosmologo Alan Guth si rese conto che i problemi del Big Bang potevano essere risolti con un add-on: uno slancio iniziale di crescita esponenziale noto come inflazione cosmica, che avrebbe reso l’universo enorme, liscio e piatto prima che la gravità avesse la possibilità di distruggerlo. L’inflazione cosmica divenne rapidamente la principale teoria delle nostre origini cosmiche. Tuttavia il problema delle condizioni iniziali rimase: qual era stata la fonte del minuscolo punto da cui si presumeva si fosse dilatato il nostro cosmo e dell’energia che continua a dilatarlo?
Hawking, che era nel suo momento di maggior fulgore, vide un modo per porre fine a questa questione senza risposta: propose che non ci fosse mai stata una fine o un inizio. Secondo la cronaca della conferenza vaticana, il fisico di Cambridge, allora 39enne e ancora in grado di parlare con la propria voce, disse agli astanti: “Ci dovrebbe essere qualcosa di molto speciale sulle condizioni dei confini dell’universo, e cosa può esserci di più speciale della condizione che non vi siano confini?“
La “proposta senza limiti“, che Hawking e il suo collaboratore, James Hartle, svilupparono ompletamente formulandola in un articolo del 1983, immagina che il cosmo abbia la forma di un volano.
Proprio come un volano ha un diametro pari a zero nel suo punto più basso e si allarga gradualmente durante la salita, l’universo, secondo la proposta senza limiti, si è espanso senza problemi da un punto di dimensioni zero. Hartle e Hawking derivarono una formula in grado di descrivere l’intero volano – la cosiddetta “funzione d’onda dell’universo” che racchiude tutto il passato, il presente e il futuro in una sola volta, rendendo discutibile ogni contemplazione di semi di creazione, un creatore o qualsiasi transizione da una volta prima.
“Chiedere cosa sia accaduto prima del Big Bang è privo di significato, secondo la proposta di no-boundary, perché non c’è nessuna nozione di tempo a cui fare riferimento“, ha spiegato Hawking in un’altra conferenza alla Pontificia Accademia nel 2016, un anno e mezzo prima la sua morte. “Sarebbe come chiedere cosa si trova a sud del Polo Sud“.

La proposta di Hartle e Hawking radicalmente riconcettualizzata
Ogni momento nell’universo diventa una sezione trasversale del volano; mentre noi percepiamo che l’universo si espande e si evolve momento dopo momento, il tempo consiste realmente di correlazioni tra le dimensioni dell’universo in ogni sezione trasversale e altre proprietà – in particolare la sua entropia, o disordine.
L’entropia aumenta continuamente, mirando a una freccia emergente del tempo. Vicino al fondo arrotondato del volano, tuttavia, le correlazioni sono meno affidabili; il tempo cessa di esistere ed è sostituito dallo spazio puro. Come Hartle, che ora ha 79 anni ed è professore all’Università della California di Santa Barbara, ha spiegato di recente, “Non c’erano uccelli nell’universo primordiale; sono venuti più tardi. E non c’era il tempo nell’universo primordiale, ma ad un certo punto è arrivato il tempo“.
La proposta del no-boundary (senza confini o senza limiti) ha affascinato e ispirato i fisici per quasi quattro decenni. “È un’idea straordinariamente bella e provocatoria“, ha detto Neil Turok , un cosmologo del Perimeter Institute for Theoretical Physics di Waterloo, Canada, ed ex collaboratore di Hawking.
La proposta ha rappresentato la prima ipotesi sulla descrizione quantistica del cosmo: la funzione d’onda dell’universo. Presto sorse un intero campo, la cosmologia quantistica che, quando i ricercatori escogitavano idee alternative su come l’universo avrebbe potuto sorgere dal nulla, analizzava le varie previsioni e le modalità delle teorie per metterle alla prova, interpretandone il significato filosofico. La funzione d’onda senza confine, secondo Hartle, “era in qualche modo la proposta più semplice possibile per rispondere a quella domanda“.
Ma due anni fa, un lavoro di Turok, Job Feldbrugge dell’Istituto perimetrale, e Jean-Luc Lehners dell’Istituto Max Planck di fisica gravitazionale in Germania, definì la proposta Hartle-Hawking. La proposta è, ovviamente, percorribile solo se un universo che si curva da un punto adimensionale nel modo in cui Hartle e Hawking immaginano si sviluppa naturalmente in un universo come il nostro.
Hawking e Hartle sostenevano che, in effetti, gli universi senza confini tenderanno ad essere enormi, incredibilmente fluidi, straordinariamente piatti e in espansione, proprio come il vero cosmo. “Il problema con l’approccio di Stephen e Jim è che era ambiguo“, ha detto Turok, “profondamente ambiguo“.
L’articolo ha scatenato una polemica. Altri esperti hanno difeso vigorosamente l’idea del no-boundary e pubblicato una confutazione del ragionamento di Turok e dei colleghi. “Non siamo d’accordo con le sue argomentazioni tecniche“, ha detto Thomas Hertog, fisico dell’Università Cattolica di Leuven in Belgio, che ha collaborato da vicino con Hawking negli ultimi 20 anni della sua vita. “Ma, fondamentalmente, non siamo d’accordo anche con la sua definizione, la sua struttura, la sua scelta di principi. E questa è la discussione più interessante“.
Dopo due anni di scaramucce, i due gruppi hanno individuato il loro disaccordo tecnico in alcune idee diverse su come funziona la natura. Il dibattito acceso, ma amichevole, ha contribuito a rafforzare l’idea che più solleticava la fantasia di Hawking. Persino i critici più accesi della formula specifica di Hawking ed Hartle, tra cui Turok e Lehners, stanno creando modelli cosmologici quantistici in competizione che cercano di evitare le presunte insidie dell’originale pur mantenendo il suo fascino sconfinato.
Il giardino delle delizie cosmiche
Hartle e Hawking si sono frequentati molto dagli inizi degli anni ’70, di solito si incontravano a Cambridge per lunghi periodi di collaborazione. Le ricerche teoriche del duo sui buchi neri e le misteriose singolarità nel loro centro li avevano trasformati nella questione della nostra origine cosmica.
Nel 1915, Albert Einstein scoprì che le concentrazioni di materia o energia deformano la trama dello spazio-tempo, a causa della gravità. Negli anni Sessanta, Hawking e il fisico dell’Università di Oxford, Roger Penrose, dimostrarono che quando lo spazio-tempo si piega abbastanza ripidamente, come all’interno di un buco nero o, forse, durante il Big Bang, inevitabilmente collassa, curvando all’infinito in modo vertiginoso verso una singolarità, dove le equazioni di Einstein non funzionano più e serve una nuova teoria quantistica della gravità.
I “teoremi delle singolarità” di Penrose-Hawking significavano che non c’è alcun modo per lo spazio-tempo di iniziare in modo uniforme, non drammatico, in un punto.
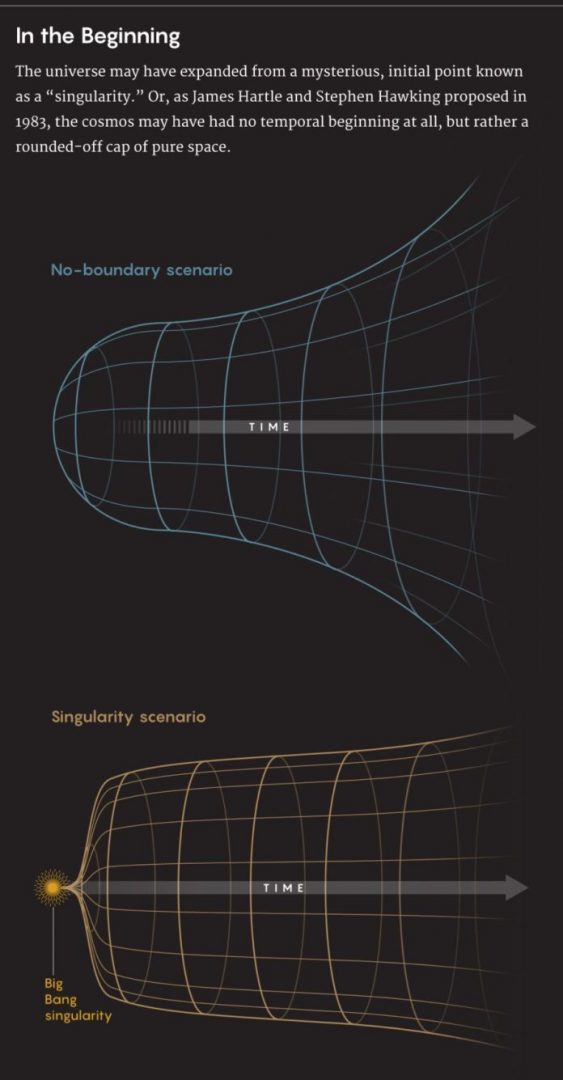
Hawking e Hartle arrivarono a riflettere sulla possibilità che l’universo fosse iniziato come spazio puro, piuttosto che come spazio-tempo dinamico. E questo li ha portati alla geometria del volano. Definirono la funzione d’onda senza confine che descrive un tale universo usando un approccio inventato dall’eroe di Hawking, il fisico Richard Feynman.
Negli anni ’40, Feynman escogitò uno schema per calcolare i risultati più probabili degli eventi di meccanica quantistica. Per prevedere, ad esempio, i risultati più probabili di una collisione tra particelle, Feynman scoprì che è possibile riassumere tutti i possibili percorsi che le particelle in collisione potrebbero prendere, ponderando i percorsi diretti più di quelli complicati nella somma. Calcolando questo “integrale del percorso” si ottiene la funzione d’onda: una distribuzione di probabilità che indica i diversi stati possibili delle particelle dopo la collisione.
Allo stesso modo, Hartle e Hawking espressero la funzione d’onda dell’universo – che descrive i suoi stati probabili – come la somma di tutti i possibili modi in cui avrebbe potuto facilmente espandersi da un punto. La speranza era che la somma di tutte le possibili “storie di espansione”, gli universi dal fondo levigato di tutte le diverse forme e dimensioni, avrebbe generato una funzione d’onda che dà un’alta probabilità a un universo enorme, liscio e piatto come il nostro. Se la somma ponderata di tutte le possibili cronologie di espansione produce un altro tipo di universo come risultato più probabile, la proposta del no-boundary fallisce.
Il problema è che l’integrale del percorso su tutte le possibili cronologie di espansione è troppo complicato per poter essere calcolato esattamente. Sono possibili innumerevoli forme e dimensioni di universi diversi, e ognuno può essere un affare disordinato. “Murray Gell-Mann era solito chiedermi“, racconta Hartle, riferendosi al compianto fisico vincitore del Premio Nobel, “se conosci la funzione d’onda dell’universo, perché non sei ricco?” Ovviamente, per risolvere effettivamente la funzione d’onda usando il metodo di Feynman, Hartle e Hawking hanno dovuto semplificare drasticamente la situazione, ignorando molte particelle specifiche che popolano il nostro mondo (il che significava che la loro formula non era affatto vicina a poter prevedere il mercato azionario).
Considerarono il percorso integrale su tutti i possibili universi in un “minisuperspace“, definito come l’insieme di tutti gli universi con un singolo campo di energia che li attraversa: l’energia che ha alimentato l’inflazione cosmica. (Nell’immagine sopra di Hartle e Hawking, quel periodo iniziale di dilatazione che corrisponde al rapido aumento del diametro vicino al fondo della campana).
Anche il calcolo del minisuperspace è difficile da risolvere esattamente, ma i fisici sanno che ci sono due possibili storie di espansione che potenzialmente dominano il calcolo. Queste forme rivali dell’universo ancorano i due lati dell’attuale dibattito.
Le soluzioni rivali sono le due storie di espansione “classiche” che l’universo può avere. A seguito di un iniziale impulso di inflazione cosmica dalla dimensione zero, questi universi si espandono costantemente secondo la teoria della gravità e dello spazio-tempo di Einstein. Le storie di espansione più strane per lo più si annullano nel calcolo quantistico.
Una delle due soluzioni classiche ricorda il nostro universo. Su grande scala, è liscia e casualmente maculata di energia, a causa delle fluttuazioni quantistiche avvenute durante l’inflazione. Come nell’universo reale, le differenze di densità tra le regioni formano una curva a campana attorno allo zero.
Se questa possibile soluzione domina davvero la funzione d’onda per il minisuperspazio, diventa plausibile immaginare che una versione molto più dettagliata ed esatta della funzione d’onda senza confine possa servire come modello cosmologico dell’universo reale.
L’altra forma di universo potenzialmente dominante non assomiglia alla realtà. Man mano che si allarga, l’energia che lo infonde varia sempre di più, creando enormi differenze di densità da un luogo all’altro che la gravità peggiora costantemente. Le variazioni di densità formano una curva a campana invertita, dove le differenze tra le regioni si avvicinano non a zero, ma all’infinito. Se questo fosse il termine dominante nella funzione d’onda senza limite per il minisuperspazio, allora la proposta di Hartle-Hawking sembrerebbe sbagliata.
Le due storie di espansione dominanti presentano una scelta su come dovrebbe essere fatto l’integrale del percorso. Se le storie dominanti sono due posizioni su una mappa, una specie di megalopoli nel regno di tutti gli universi di meccanica quantistica possibili, la domanda è quale percorso dovremmo percorrere attraverso il terreno.
Quale sarà la storia di espansione dominante, e ce ne può essere una sola, se il nostro “contorno dell’integrazione” dovesse emergere? I ricercatori hanno biforcato diversi percorsi.
Nel loro articolo del 2017, Turok, Feldbrugge e Lehners hanno intrapreso un percorso attraverso una mappa delle possibili storie di espansione che ha portato alla seconda soluzione dominante. Dal loro punto di vista, l’unico contorno sensibile è quello che analizza i valori reali (in contrapposizione ai valori immaginari, che coinvolgono le radici quadrate dei numeri negativi) per una variabile chiamata “intervallo“.
L’intervallo è essenzialmente l’altezza di ogni possibile universo a volano – la distanza necessaria per raggiungere un certo diametro. Mancando di un elemento causale, l’errore non è la nostra solita nozione di tempo. Eppure Turok e colleghi discutono in parte sulla base della causalità sostenendo che solo i veri valori di decadenza hanno senso fisico. E riassumere gli universi con i veri valori di decadenza conduce ad una soluzione fluttuante, fisicamente priva di senso.
“La gente ripone grande fiducia nell’intuizione di Stephen“, ha spiegato Turok. “Per una buona ragione – voglio dire, probabilmente ha avuto la migliore intuizione di chiunque su questi argomenti. Ma non ha sempre ragione“.
Universi immaginari
Jonathan Halliwell, un fisico dell’Imperial College di Londra, ha studiato la proposta di no-bound da quando era studente di Hawking negli anni ’80. Lui e Hartle hanno analizzato il problema del profilo dell’integrazione nel 1990. Dal loro punto di vista, così come quello di Hertog e, apparentemente, di Hawking, il contorno non è fondamentale, ma piuttosto uno strumento matematico che può essere sfruttato a proprio vantaggio. È simile a come la traiettoria di un pianeta attorno al sole può essere espressa matematicamente come una serie di angoli, come una serie di volte, o in termini di uno qualsiasi dei molti altri parametri convenienti. “Puoi eseguire questa parametrizzazione in molti modi diversi, ma nessuno di questi, in fisica, è più valido di un altro“, ha detto Halliwell.
Lui ed i suoi colleghi sostengono che, nel caso del minisuperspace, solo i contorni che riprendono la storia di espansione giusta hanno senso. La meccanica quantistica richiede che le probabilità aumentino a 1, o siano “normalizzabili”, ma l’universo fluttuante su cui la squadra di Turok è atterrata non lo è.
Quella soluzione è priva di senso, afflitta da infiniti e non consentita dalle leggi quantistiche.

È vero che i contorni che attraversano la soluzione giusta riassumono possibili universi con valori immaginari per le loro variabili di intervallo, Ma, a parte Turok e compagnia, poche persone pensano che sia un problema. I numeri immaginari pervadono la meccanica quantistica. Per il gruppo pro ipotesi Hartle-Hawking, i critici stanno invocando una falsa nozione di causalità nel richiedere che tale errore sia reale. “Questo è un principio che non è scritto nelle stelle, e con il quale siamo profondamente in disaccordo“, ha detto Hertog.
Secondo Hertog, Hawking raramente menzionava la formulazione integrale del percorso della funzione d’onda senza limiti negli ultimi anni, in parte a causa dell’ambiguità intorno alla scelta del contorno. Considerava la storia dell’espansione normalizzabile, che l’integrale del percorso aveva semplicemente contribuito a scoprire, come la soluzione a un’equazione più fondamentale sull’universo posta negli anni ’60 dai fisici John Wheeler e Bryce DeWitt.
Wheeler e DeWitt sostenevano che la funzione d’onda dell’universo, qualunque essa sia, non può dipendere dal tempo, poiché non esiste un orologio esterno con cui misurarla. E quindi la quantità di energia nell’universo, quando si sommano i contributi positivi e negativi di materia e gravità, deve rimanere a zero per sempre.
Negli ultimi anni della sua vita, per comprendere meglio la funzione d’onda, Hawking ed i suoi collaboratori hanno iniziato ad applicare l’olografia, un nuovo approccio di grande successo che tratta lo spazio-tempo come un ologramma.
Hawking cercava una descrizione olografica di un universo a forma di volano, in cui la geometria dell’intero passato si proiettava fuori dal presente.
Questo sforzo continua anche in assenza di Hawking. Ma Turok vede questo spostamento di enfasi come un cambio delle regole. Nell’abbandonare la formulazione integrale del percorso, afferma, i sostenitori dell’idea no-boundary lo hanno reso mal definito. Quello che stanno studiando non è più Hartle-Hawking, a suo parere – sebbene lo stesso Hartle non sia d’accordo.
Nell’ultimo anno, Turok e i suoi colleghi, Latham Boyle e Kieran Finn hanno sviluppato un nuovo modello cosmologico che ha molto in comune con la proposta del no-boundary. Ma invece di un volano, immagina due tappi di sughero posizionati a tappare una specie di figura a clessidra con il tempo che scorre in entrambe le direzioni.
Mentre il modello non è ancora sufficientemente sviluppato per fare previsioni, il suo fascino sta nel modo in cui i suoi lobi realizzano la simmetria CPT, uno specchio apparentemente fondamentale nella natura che riflette simultaneamente la materia e l’antimateria, sinistra e destra, e avanti e indietro nel tempo.
Uno svantaggio è che i lobi dell’immagine speculare dell’universo si incontrano in una singolarità, un “punto” nello spazio-tempo che richiede la comprensione della teoria quantistica della gravità. Boyle, Finn e Turok prendono a pugnalate la singolarità, ma un simile tentativo è intrinsecamente speculativo.
C’è stata anche una rinascita di interesse per la “proposta di tunneling“, un modo alternativo attraverso il quale l’universo avrebbe potuto sorgere dal nulla, concepito negli anni ’80 dai cosmologi russo-americani Alexander Vilenkin e Andrei Linde. La proposta, che differisce dalla funzione d’onda senza limiti principalmente per mezzo di un segno meno, ipotizza la nascita dell’universo come un evento di “tunneling” quantistico, simile a quando una particella attraversa una barriera in un esperimento di meccanica quantistica .
Le domande abbondano su come le varie proposte si intersecano con il ragionamento antropico e l’infame idea del multiverso. La funzione d’onda senza confine, ad esempio, favorisce gli universi vuoti, mentre sono necessari materia ed energia significative per alimentare l’enormità e la complessità.
Hawking sostenne che l’enorme numero di possibili universi consentiti dalla funzione d’onda deve essere realizzata in un grande multiverso, all’interno del quale solo universi complessi come il nostro avranno abitanti capaci di fare osservazioni. (Il recente dibattito riguarda se questi universi complessi e abitabili saranno lisci o fluttuanti).
Un vantaggio della proposta del tunneling è che favorisce universi ricchi di materia ed energia come i nostri senza ricorrere al ragionamento antropico – sebbene universi che scavalcano l’esistenza potrebbero avere altri problemi.
Non importa come andranno le cose, forse rimarremo con qualche aspetto della teoria che Hawking presentò alla Pontificia Accademia delle Scienze 38 anni fa. O forse, al posto di un non-inizio, scopriremo che l’universo è emerso da una singolarità, dopotutto, richiedendo un diverso tipo di funzione d’onda.
In ogni caso, la ricerca continuerà. “Se stiamo parlando di una teoria della meccanica quantistica, cos’altro c’è da trovare oltre alla funzione d’onda?“, Ha chiesto Juan Maldacena, un eminente fisico teorico dell’Institute for Advanced Study di Princeton, nel New Jersey, che è rimasto per lo più fuori dalla recente mischia.
La questione della funzione d’onda dell’universo “è il giusto tipo di domanda da porre“, ha detto Maldacena, che, per inciso, è membro della Pontificia Accademia. “Se stiamo trovando la giusta funzione d’onda, o come dovremmo pensare alla funzione d’onda, è meno chiaro“.
Fonte: Quanta Magazine




Lascia un commento