
La letalità apparente e quella reale di COVID-19. I dati sulla pandemia comunicati dalle autorità di tutti i paesi colpiti hanno finito per generare nella popolazione una notevole confusione su quale sia l’effettivo andamento della pandemia. Qui, quattro scienziati esperti nel maneggiare dati statistici e modelli offrono una chiave di lettura per chiarire la complessa relazione fra la cosiddetta letalità apparente di COVID-19 e quella reale.
I dati relativi alla pandemia di Covid-19, forniti per esempio dalla John Hopkins University, mostrano che la letalità apparente, dipendente dal tempo (definita come il numero cumulato di decessi fino a un dato momento diviso per il numero cumulato di persone trovate infette fino allo stesso momento) cresce con il passare dei giorni in molti paesi. Possiamo per esempio partire dalla constatazione del fatto che in Italia la letalità apparente è cresciuta del 20 per cento nell’ultimo mese.
E’ opportuno cominciare con alcune osservazioni preliminari e cautelari. In primo luogo, non abbiamo motivo di credere che quella che qui chiamiamo “letalità apparente” sia in qualche modo vicina alla vera letalità dovuta al Covid-19.
Non sappiamo affatto quanti individui siano stati realmente infettati dal virus (e questa è, allo stato attuale dell’evoluzione della pandemia, una delle cose che vorremmo davvero sapere quanto prima). Quello che conosciamo è il numero di risposte positive che otteniamo dai test effettuati in un dato numero giornaliero secondo un protocollo specifico. Il numero reale di persone infette è sicuramente molto più grande e, di conseguenza, la vera letalità è probabilmente più piccola di quella che citiamo qui.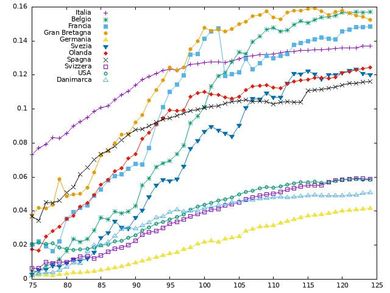
Questo non è un problema per il nostro ragionamento, poiché non ci interessa una normalizzazione assoluta, purché i protocolli usati per i test non cambino troppo nel tempo (a volte sono cambiati nel passato e questo si vede leggermente in alcuni dati, senza produrre, tuttavia, nessun effetto importante, tale da invalidare il nostro ragionamento).
Possiamo inoltre confrontare diversi paesi a condizione che i protocolli usati per i test in questi paesi e il numero di test eseguiti non sia troppo diverso (in pratica un po’ diversi lo sono e questo può, di sicuro, spiegare alcune delle differenze che osserviamo; commenteremo ulteriormente su questo).
Di recente si è discusso del fatto che anche il numero di decessi è sicuramente sottostimato, ma probabilmente di un fattore minore rispetto alle persone infette. Il numero dei decessi potrebbe essere in media sottovalutato di un fattore vicino a due o più piccolo, mentre il numero degli infetti è probabilmente sottostimato di una quantità molto grande, che ci aspettiamo possa dipendere fortemente dal tempo.
È chiaro che l’aumento della letalità nel tempo non corrisponde alle nostre aspettative e, se fosse reale, sarebbe una pessima notizia. Durante la crisi pandemica si sviluppano nuove competenze, l’uso appropriato dei farmaci viene migliorato grazie all’esperienza clinica, e anche la crisi che alcuni sistemi sanitari hanno vissuto in diversi paesi non può spiegare una crescita persistente della letalità.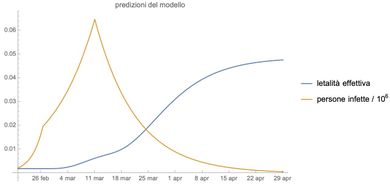
Nella figura 1 mostriamo la letalità apparente per diversi paesi in funzione del tempo (sull’asse delle x riportiamo il giorno dell’anno). Si vede subito che c’è un chiaro e forte aumento di questa letalità stimata, dipendente dal tempo, per tutti i paesi che abbiamo analizzato. La letalità complessivamente si estende su una vasta gamma di valori (e questo può dipendere in parte dal modo in cui i diversi paesi misurano e segnalano le persone infette e i decessi legati a COVID-19), ma per tutti i paesi l’aumento è chiaro e sostanziale.
I dati hanno caratteristiche interessanti: per esempio, nei paesi con una bassa letalità apparente si osservano fluttuazioni intrinseche molto più piccole rispetto alla maggior parte dei paesi ad alta letalità, come si può notare confrontando per esempio i dati per la Germania o la Svizzera con quelli per la Svezia o la Francia (il Belgio include sistematicamente fra i decessi Covid-19 i cosiddetti “casi sospetti”, e cioè le morti con chiari sintomi Covid-19 ma senza certificazione).
Nel periodo di 50 giorni mostrato in figura 1 la letalità stimata cresce di un fattore enorme, per esempio circa tre per la Spagna e circa quattro per il Regno Unito. Questo non ha alcun senso a prima vista. Nel seguito diamo una spiegazione molto ragionevole di ciò che crediamo stia realmente accadendo, e vedremo che ha davvero senso: non possiamo essere sicuri che sia la risposta giusta, ma crediamo che sia un’ipotesi molto appropriata. Esattamente lo stesso argomento può essere applicato alla situazione di Wuhan, all’inizio dell’epidemia, quando la letalità è stata stimata tra il 4 e il 5 per cento (rispetto allo 0,9 per cento del resto della Cina).
Cerchiamo quindi di capire perché la letalità apparente dipende così tanto dalla data. Daremo qui una spiegazione qualitativa, ma le formule a sostegno del nostro ragionamento non sono troppo complicate.
Ipotizziamo, per semplificare l’esposizione, che i decessi arrivino sempre 12 giorni dopo che la malattia è stata confermata da un test (si tratta di una semplificazione eccessiva, poiché il ritardo effettivo varia molto da un paziente all’altro, ma i risultati non dipendono da questo presupposto). Si assuma anche per semplicità (è banale generalizzare il ragionamento a situazioni diverse) che nella fase iniziale delle epidemie il numero di persone infette raddoppi ogni tre giorni (la cosiddetta crescita esponenziale con un tempo di raddoppio pari a 3 giorni).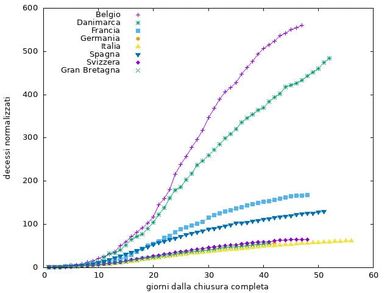
Questi sono numeri arbitrari, che non hanno a che fare con la realtà, e sono utili solo a discutere il nostro esempio in modo semplice. Quindi se avessimo, per esempio, una vera letalità dell’1 per ci aspetteremmo di vedere oggi un numero di morti pari al numero di persone che si sono sottoposte al test dodici giorni fa moltiplicato per 0,01.
Questo se ipotizziamo di avere una perfetta efficienza del nostro sistema di test (una situazione ideale molto diversa da quella reale), dove ogni giorno controlliamo l’intera popolazione, tale che il numero di infezioni rilevate sia pari al numero reale di infezioni. In questo caso il numero di infezioni (rilevate e reali) 12 giorni prima era 16 volte inferiore al numero di infezioni che abbiamo oggi (il raddoppio è ogni tre giorni, e in 12 giorni abbiamo il tempo di avere 4 raddoppi, cioè un fattore 2 per 2 per 2 per 2 per 2, che è pari a 16). Quindi nelle condizioni di una crescita esponenziale, la letalità apparente che misureremmo con un perfetto rilevamento delle infezioni e dei decessi è 1/16 del vero 1 per, cioè, 0,0625 per cento.
Ora, che cosa succede quando l’aumento esponenziale rallenta, per esempio grazie alle misure di contenimento e alla fine dell’epidemia che tutti sperano si avvicini? E’ chiaro che in questa situazione la letalità apparente stimata dividendo il numero dei morti per il numero dei contagiati nello stesso giorno si avvicina al valore reale. Quindi la letalità diventa accuratamente stimata su tempi lunghi.
Ripetiamo che nel nostro caso abbiamo un fattore costante tra letalità apparente e letalità reale di cui non possiamo rendere conto, poiché non conosciamo realmente il numero di persone infette. Ma quello che possiamo dire è che quando siamo fuori dal regime di crescita esponenziale le stime giorno per giorno della letalità tendono a una costante, che saremo in grado di connettere alla vera letalità di Covid-19 quando avremo una stima corretta del numero di infezioni.
In questo modo il regime di crescita esponenziale provoca una sottostima della letalità e quando la crescita esponenziale si arresta, allora la letalità apparente deve aumentare e avvicinarsi a un plateau. L’appiattimento della letalità apparente, dipendente dal tempo, è quindi un segnale che l’epidemia è in uno stato stabile, e che la sua velocità di propagazione ha smesso di crescere. E questo è il caso di tutti i paesi con una elevata letalità apparente (quelli mostrati nella parte superiore della figura 1).
L’evoluzione per i paesi con letalità apparente molto bassa (per esempio Germania, Svizzera e Stati Uniti) è più fluida, per cui la distinzione tra il regime di crescita e il plateau è meno chiara. Tuttavia il risultato generale che si trova, e questo è notevole, è che l’aumento della letalità apparente è legato alla diminuzione della forza della epidemia. Anche in questo caso, il fatto che il valore stimato sia elevato non è rilevante finché non si misura con buona precisione il numero di infezioni: probabilmente quando saremo in grado di ottenere stime precise si scoprirà che il numero di infezioni è sottostimato di un fattore di ordine dieci.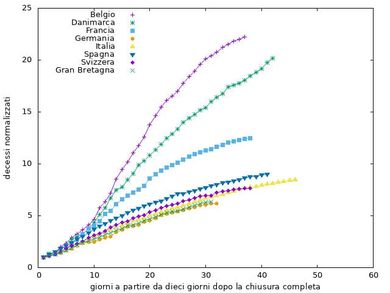
Possiamo avvalorare il nostro ragionamento grazie a un modello molto semplice che è stato recentemente proposto per descrivere il rallentamento dell’epidemia dopo il lockdown totale. Questo modello matematico, così come applicato in Italia, è stato utile per cercare di stimare gli effetti del lockdown (che a livello nazionale è iniziato in Italia l’11 marzo 2020); il modello è stato usato per quantificare la situazione il 10 aprile e in quel giorno ha dato una descrizione molto accurata della situazione, e risultati coerenti.
In sintesi, in questo modello si implementa una crescita esponenziale prima del lockdown con due diversi tassi di crescita: una crescita più rapida prima della chiusura delle cosiddette “zone rosse” (26 febbraio) e una più lenta dopo tale data. I due tassi di crescita sono stati ricavati dai dati. Dopo la chiusura completa sono stati proposti quattro diversi scenari, con l’epidemia che decresce con tassi diversi, e lo scenario ottimale è stato determinato dalla consistenza con i dati reali. Il 10 aprile la risposta alla domanda è stata che sì, il modello descriveva in modo molto accurato i dati disponibili, usando un tempo di 7 giorni per il dimezzamento dei nuovi casi giornalieri (probabilmente questo numero sarebbe leggermente più alto se venisse stimato oggi). Con la curva arancione della figura 2 mostriamo l’evoluzione del numero di persone infette nel modello (riscalate di un fattore di un milione).
Per verificare le idee che presentiamo qui abbiamo calcolato la letalità apparente, dipendente dal tempo, che un tale modello, addestrato sui dati reali, implicherebbe. Abbiamo diviso il numero di decessi previsti dal modello per il numero di casi positivi rilevati. Anche in questo caso non conosciamo la normalizzazione globale del numero di infezioni, e possiamo solo guardare come cambiano nel tempo: la scala globale è, quindi, arbitraria. Mostriamo la letalità apparente, dipendente dal tempo, predetta dal modello in figura 2 con una curva blu. Esattamente come avviene nei dati reali la letalità apparente stimata dal modello cresce con il tempo dopo il lockdown quando l’epidemia sta rallentando. Crediamo che questo, si spera, chiarisca completamente la situazione della crescita della letalità apparente.
Aggiungiamo anche una seconda osservazione, cercando di quantificare l’effetto del blocco nei diversi paesi. Analisi molto interessanti sugli effetti di chiusura totale sono state fatte da Serena Bradde e Benedetta Cerruti e da Pedro Fonseca. Loro usano una normalizzazione diversa dalla nostra, ottenendo risultati complementari ai nostri. Ancora una volta basiamo la nostra analisi sui dati raccolti dalla John Hopkins University, mentre otteniamo le date del blocco dal Lockdown Tracker di Aura Vision (per la Germania usiamo il 23 marzo come data della chiusura totale, visto che solo in quel giorno la grande maggioranza dei Laender ha implementato misure completamente restrittive).
In che modo l’isolamento ha influenzato la progressione del numero di morti? Per verificare i nostri risultati, normalizziamo il numero totale di morti sia al numero di morti al momento dell’isolamento (se l’isolamento è stato implementato a zero morti, lo normalizziamo a uno) sia al numero di morti al decimo giorno dopo l’isolamento. Mostriamo le due serie di curve nelle figure 3 e 4.
Le figure 3 e 4 sono in effetti molto simili, a dimostrazione del fatto che la scelta del momento che usiamo per normalizzare i nostri dati è ragionevolmente irrilevante. Vediamo che un gruppo di paesi (Germania, Italia, Svizzera, Regno Unito e in qualche misura Spagna) sembra aver reagito in modo molto simile, mentre in altri paesi la crescita del numero di morti rispetto al giorno dell’isolamento (o a dieci giorni dopo) è stata più rapida. Chiaramente ci sono possibili fonti di grande errore e diversi modi di leggere questi dati di isolamento, ma riteniamo che l’analisi di questo comportamento offra prospettive interessanti.
Questa nota è stata scritta utilizzando i dati del 3 maggio 2020, provenienti dall’archivio github. Si ringrazia calorosamente Marco Cattaneo per una conversazione molto interessante che ha contribuito a motivare questo lavoro e per un’attenta e gentile lettura del nostro manoscritto, e Benedetta Cerruti per interessanti conversazioni e utili consigli.
Gli autori:
Luca Leuzzi, fisico teorico, è ricercatore all’Istituto di nanotecnologie CNR-Nanotec di Roma e insegna all’Università di Roma “Sapienza”.
Enzo Marinari insegna fisica all’Università di Roma “Sapienza”, e svolge attività di ricerca all’Istituto di nanotecnologie CNR-Nanotec di Roma e alla sezione di Roma1 dell’INFN.
Giorgio Parisi professore emerito all’Università Sapienza di Roma, svolge attività di ricerca all’Istituto di nanotecnologie CNR-Nanotec di Roma e alla sezione di Roma1 dell’INFN.
Federico Ricci-Tersenghi insegna fisica all’Università di Roma “Sapienza”, e svolge attività di ricerca all’Istituto di nanotecnologie CNR-Nanotec di Roma e alla sezione di Roma1 dell’INFN.



Lascia un commento