Numerologia Orientale e Feng Shui degli I Ching

Condividi l'Articolo

Le basi matematiche dell’I Ching.

Riportati alcuni estratti da un articolo del 1974 di Martin Gardner sull’analisi combinatoria del Libro dei Mutamenti

L’I Ching, o Libro dei Mutamenti, è uno dei più antichi libri del mondo ed anche uno dei più enigmatici. Per più di 2000 anni è stato usato in Oriente come libro di divinazione ed è tuttora studiato con rispettosa deferenza come sorgente della saggezza confuciana e taoista.
[…]
Il fondamento combinatorio dell’I Ching consiste in 64 esagrammi. Essi mostrano ogni possibile permutazione di due tipi di linee prese sei alla volta. Ogni esagramma ha un nome tradizionale cinese. I due tipi di linee rappresentano la dualità di base della metafisica cinese: la linea spezzata corrisponde allo yin, la linea intera allo yang. Prendendo 2 linee alla volta ci sono 2×2 = 4 possibilità di combinarle formando i cosiddetti digrammi e 2x2x2 = 8 possibilità di formare trigrammi.
[…]
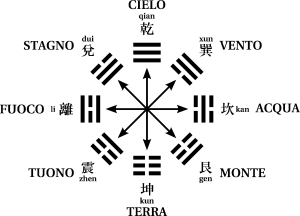
Ci sono due modalità antiche per rappresentare gli otto trigrammi in un cerchio. La più antica, conosciuta come disposizione di Fu Xi dal nome del mitico fondatore della prima dinastia cinese (la dinastia Xia, 2205-1766 a.C.) è riportata qui di fianco. Si noti che le coppie opposte sono complementari sia per quanto riguarda il significato simbolico che dal punto di vista matematico poichè ogni elemento si ottiene dall’altro sostituendo le linee yin con le yang e le linee yang con le yin. Questa disposizione, che solitamente incornicia il famigliare simbolo dello yin-yang, è tuttora largamente utilizzata in Cina, Giappone e Corea come augurio di buona fortuna da appendere sulla porta o da riprodurre sui gioielli. E’ anche chiamata “cielo anteriore” o “disposizione primaria”. 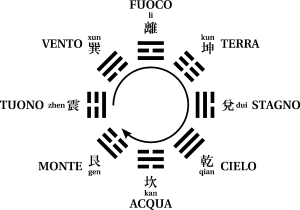La disposizione di Re Wen (dal nome del leggendario padre del fondatore della dinastia Zhou), riprodotta qui di fianco (detta anche “cielo posteriore” o “disposizione del mondo interiore”), abbandona il posizionamento complementare della sequenza di Fu Xi, di modo che i trigrammi posti ai punti cardinali della bussola simbolizzano le stagioni in ordine ciclico. Partendo dal sud ☲ (tradizionalmente mostrato in alto) e muovendosi in senso orario i trigrammi disposti ai punti cardinali rappresentano estate ☲, autunno ☱, inverno ☵ e primavera ☳.La più antica disposizione dei 64 esagrammi, che è conosciuta come sequenza di Re Wen, è l’ordine in cui essi appaiono nell’I Ching (si veda l’immagine riportata qui di seguito).
[…]

Si noti che gli esagrammi sono appaiati in un modo singolare. Ogni esagramma dispari è seguito da un esagramma che è o il suo inverso o il suo complementare. Se l’esagramma dispari è simmetrico (rimane uguale anche se rovesciato), viene complementato per produrre l’esagramma successivo. Se manca di simmetria, viene invertito.

C’è un qualche tipo di ordinamento matematico che determina la sequenza in cui le coppie di esagrammi si susseguono l’un l’altra? Questo è un problema irrisolto. Di volta in volta uno studioso dell’I Ching annuncia di aver scoperto uno schema matematico sottostante la sistemazione delle coppie, ma ogni volta un’indagine più ravvicinata rivela che sono state fatti tanti e tali assunti arbitrari da far in modo che in effetti l’ordine fosse imposto prima che esso emergesse dall’analisi. Per quanto si possa conoscere, le coppie dell’ordinamento di Re Wen sono disposte in ordine casuale e non vi sono basi conosciute per determinare quale membro di una coppia preceda l’altro.

Solo nell’undicesimo secolo gli studiosi cinesi scoprirono una modalità di ordinamento degli esagrammi molto semplice ed elegante. Questa sistemazione è attribuita a Fu Xi (si veda l’illustrazione riportata qui di seguito).

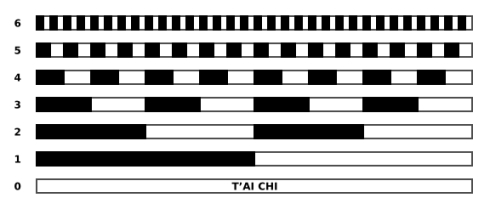
Lo spazio bianco in basso rappresenta il Tai Chi, lo stato dell’universo quando era “senza forma, e vuoto” (come riporta Genesi 1:2). Questo caos indifferenziato si divide nelle metà yin (nera) e yang (bianca) della riga 1. Nella riga 2 vediamo lo yin suddividersi in yin e yang e similmente lo yang. Questa suddivisione binaria continua per sei passi verso l’alto.
Lo schema ora rivela automaticamente tutti i poligrammi di ordine da 1 a 6. Dividendo le righe 1 e 2 verticalmente in quattro parti uguali e rimpiazzando in ciascuna parte il nero con la una linea spezzata ed il bianco con una linea intera si ottengono i quattro digrammi. Le righe 1, 2 e 3 divise verticalmente in otto parti uguali generano gli otto trigrammi. Le righe 1, 2, 3 e 4 in 16 parti danno i 16 tetragrammi, le righe 1, 2, 3, 4 e 5, in 32 parti danno i 32 pentagrammi, e le righe 1, 2, 3, 4, 5 e 6, in 64 parti, danno i 64 esagrammi.

La Matrice del Destino

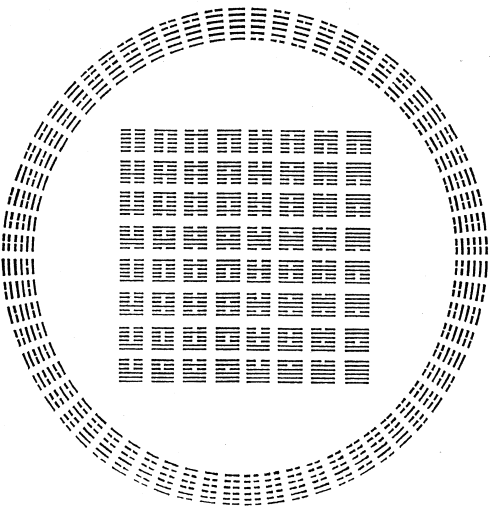
L’illustrazione successiva mostra gli esagrammi nel loro tradizionale ordine di Fu Xi, o “naturale.

Procedendo da sinistra a destra, a partire dalla prima riga del quadrato, gli esagrammi corrispondono a quelli riportati nello schema di Fu Xi letto sempre da sinistra a destra.

Possiamo ora capire perchè Leibniz, che pensava di aver inventato il sistema binario alla fine del 17° secolo, fosse così stupefatto dopo aver appreso per la prima volta della sequenza di Fu Xi da Padre Bouvet, un missionario gesuita in Cina. Sostituiamo 0 ad ogni linea spezzata, 1 ad ogni linea intera, poi prendiamo gli esagrammi in ordine, leggendo ognuno di essi dal basso verso l’alto ed otteniamo la sequenza: 000000, 000001, 000010, 000011, …, 111111. Non si tratta di nient’altro che di contare i numeri da 0 a 63 espressi in notazione binaria.
Sia Leibniz che Padre Bouvet erano convinti che Fu Xi, colpito dall’ispirazione divina, avesse scoperto l’aritmetica binaria, ma non c’è nessuna chiara evidenza di questo. Gli studiosi dell’I Ching dell’11° secolo non avevano fatto niente di più che scoprire una modalità naturale di disporre gli esagrammi. Non fu che al tempo di Leibniz che la sequenza di Fu Xi venne riconosciuta isomorfa ad un’utile notazione aritmetica.

Poichè il potere del 2 si esplica ovunque nelle strutture matematiche e fisiche, non è sorprendente che gli studiosi cinesi siano stati capaci di applicare gli esagrammi praticamente a qualunque cosa, dalla struttura dei cristalli al sistema solare ed al cosmo. Z.D. Sung, nel suo dilettevole libretto The Symbols of Yi King (Shanghai, The China Modern Education Company, 1934), racconta come stava facendo ruotare una scatola di cerini in mano un giorno (per simulare la rotazione della Terra in orbita attorno al sole) quando improvvisamente percepì un modo naturale per generare gli otto trigrammi agli angoli di un cubo.

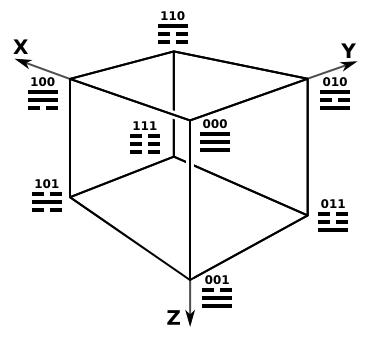Supponendo che le tre coordinante cartesiane di un cubo unitario, x, y e z, indichino la prima, la seconda e la terza cifra di un numero binario a 3 cifre, indichiamo con 000 l’angolo d’origine delle coordinante. Gli altri angoli corrispondono ai numeri binari di tre cifre da 0 a 7, dove 0 e 1 indicano la distanza dell’angolo dall’origine di ogni linea coordinata. Gli otto numeri corrispondono, naturalmente, agli otto trigrammi, con i trigrammi complementari disposti agli angoli diametricalmente opposti del cubo. Con una procedura siile gli angoli di un ipercubo unitario genera i poligrammi di ordine superiore.
Invece di avventurarsi nelle dimensioni superiori, Sung divide il cubo in 64 cubi più piccoli che egli identifica con i 64 “modi” del sillogismo classico. (La premessa maggiore, la premessa minore e la conclusione di un sillogismo possono prendere ognuna quattro forme differenti generando 64 possibili modi.)
[…]